| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 브루트포스
- 프로그래머스
- 코딩테스트
- 정렬
- 완전탐색
- hash
- 자바스크립트
- 병합 정렬
- BOJ
- useState
- CSS
- 딥다이브
- 자료구조
- 코테
- Node
- node.js
- JavaScript
- 연결리스트
- state
- 백준
- react
- 합병 정렬
- sort
- 알고리즘
- 리액트
- JS
- 최소공배수
- 해시
- 정규표현식
- 기술면접
- Today
- Total
가치투자자
[프로그래머스] k진수에서 소수 개수 구하기 본문
Programmers : k진수에서 소수 개수 구하기

🔗 문제 링크
https://school.programmers.co.kr/learn/courses/30/lessons/92335
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
💬 문제
이 문제는 진수변환 과 소수(prime number) 가 무엇인지 알고 있으면 풀 수 있는 문제며, 어떻게 푸느냐에 따라 효율성이 달라졌다.
1. 양의 정수 n을 k진수로 변환했을 때, 변환된 수 내에 아래의 조건에 맞는 소수가 몇 개가 있는지 찾아야 한다.
- 0소수0 : 소수 양쪽에 0이 있는 경우
- 소수0 : 소수 오른쪽에만 0이 있는 경우
- 0소수 : 소수 왼쪽에만 0이 있는 경우
- 소수 : 소수만 있는 경우
2. 위 조건을 쉽게 해석해보면, 소수 양쪽에 0이 있을 수도 있고 없을 수도 있는 모든 경우다.
- 0이 기준이 되므로, 0을 기준으로 변환된 n을 잘랐을 때 소수가 몇 개가 있는지 파악하면 된다
- 소수 내에 0이 포함되어서는 안 되므로, 0을 제거해줘도 상관없다

💡 입출력 예시
1번째 예시에서 437674를 3진법으로 변환하면 211020101011이 된다.
0을 기준으로 잘라주면, [211, 2, 1, 1, 11]이 된다. 1은 소수가 아니므로 여기에서 소수는 211, 2, 11이다.
2번째 예시는 10진법이므로 그대로 110011이다.
0을 기준으로 잘라주면, [11, 11]이 된다. 여기서 소수는 11, 11이다.
이때 주의할 점은 110011을 0을 기준으로 잘라주면 ['11', '', '11']로 빈 문자열이 포함되며, 빈 문자열을 정수화하면 0으로 변환되므로 이 역시 고려해줘야 한다.

💻 풀이
총 2가지 방식으로 풀어보았다.
🔑 풀이1 : Math.sqrt
정수 N이 소수인지 판별하기 위한 가장 일차원적인 방법은 "N보다 작은 모든 자연수로 N을 나눠보는 것"이다.
그러나 이 판별법은 N 미만의 모든 자연수로 나눈다는 점에서 비효율적이다.
이것보다 나은 방법은 "√N 이하의 모든 자연수들로 N을 나눠보는 것"이다.
N이 16일 때, N은 아래처럼 두 수의 곱으로 이루어져있다.
1 X 16
2 X 8
4 X 4
8 X 2
16 X 1
1부터 15까지의 수로 16을 나눴을 때, 2로 16이 나눠진다는 것은 8로도 16이 나눠진다는 것을 의미한다.
따라서 √N 보다 큰 수로 중복 검사되는 것을 막기 위해 √N까지만 검사하는 것이다.
💬 문제 풀이
- n을 k진법으로 변환하고 0을 기준으로 잘라준다.
- 잘려진 수들을 돌면서 각 수 num을 소수 판별 함수 isPrime에 넣어준다
- true를 반환할 경우에는 num이 소수라는 것이므로 count를 증가시켜준다 - isPrime 함수
- 소수가 아닌 0과 1은 false로 반환해준다
- 2부터 √N 미만의 모든 자연수로 num을 나눴을 때, 약수가 있다면 소수가 아니므로 false를 반환해준다
- √N 이하의 모든 자연수로 나눠도 약수가 없을 경우는 num이 소수이므로 true를 반환해준다
function solution(n, k) {
let count = 0;
n.toString(k).split("0")
.map((num) => {
if (isPrime(Number(num))) {
count++;
}
});
return count;
}
function isPrime(num) {
if (num <= 1) {
return false;
}
for (let i=2; i <= Math.sqrt(num); i++) {
if (num % i === 0) { // 약수가 있다면 소수가 아니다
return false;
}
}
return true;
}
실행 결과와 채점 결과는 다음과 같다.


🔑 풀이2 : 에라토스테네스의 체
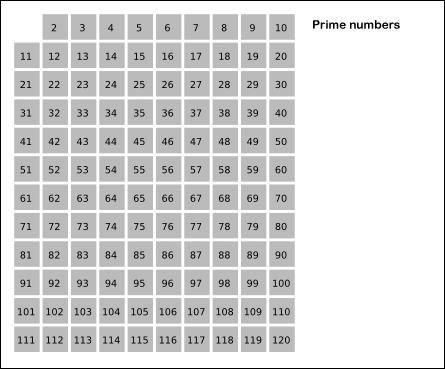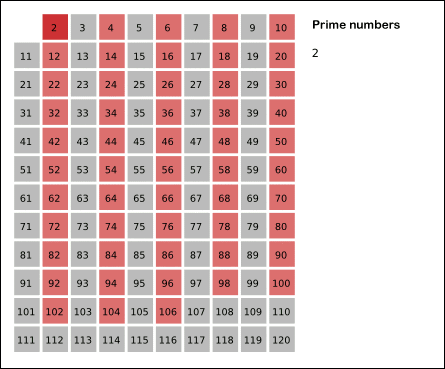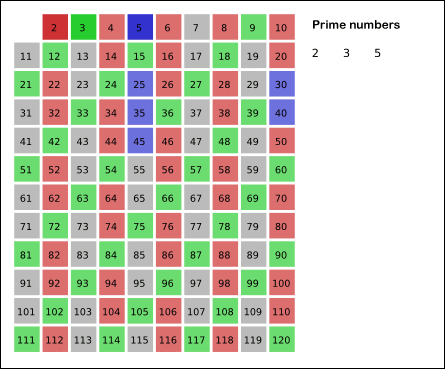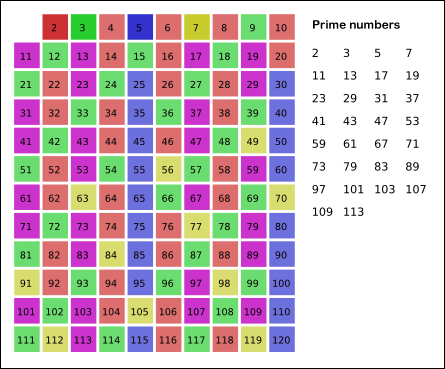
소수를 찾는 대표적인 방법 중 하나인 "에라토스테네스의 체"로 풀어보았다.
"에라토스테네스의 체"는 a의 배수들은 a를 약수로 가지고 있어 소수가 아니므로, a의 배수들을 모두 제외시키는 방법이다.
💬 문제 풀이
- n을 k진법으로 변환하고 0을 기준으로 잘라주고, 정수화해준다.
- 에라토스테네스의 체로 소수가 아닌 수들을 가려내기 위해 정수들 중 가장 큰 수를 MAX로 뽑아준다. - 에라토스테네스의 체
- 0과 1은 소수가 아니므로 true로 noPrime에 넣어준다
- 2부터 MAX의 제곱근 범위까지 돌면서 모든 소수가 아닌 모든 수를 true로 넣어준다
- i의 배수들은 모두 true로 들어간다. - num 중에서 noPrime에 들어가 있지 않다면 소수이므로, count를 증가시켜준다.
function solution(n, k) {
let count = 0;
const arr = n.toString(k).split("0").map(Number);
const MAX = Math.max(...arr);
// 에라토스테네스의 체
const noPrime = { 0: true, 1: true };
for (let i=2; i <= Math.sqrt(MAX); i++) {
if (noPrime[i]) {
continue;
}
for (let j = i * i; j <= MAX; j += i) {
noPrime[j] = true;
}
}
arr.map((num) => {
if (!noPrime[num]) {
count++;
}
});
return count;
}
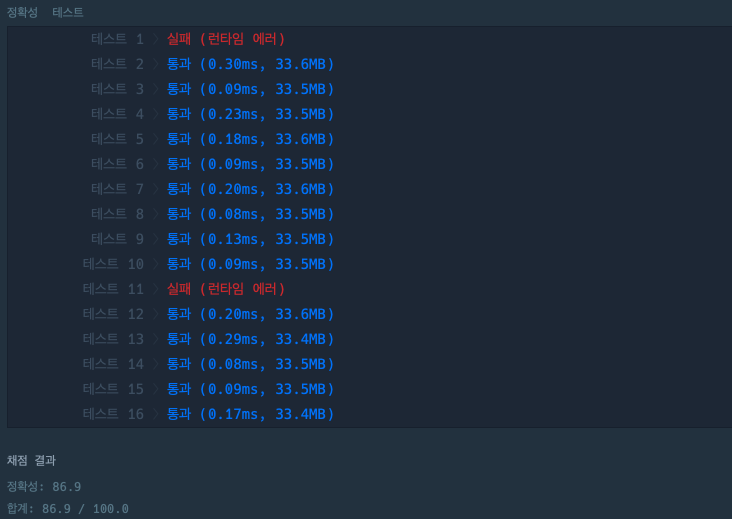
예시 케이스는 모두 정상적으로 통과했다.
그러나 몇몇 케이스에서는 런타임 에러가 발생했다. 1번째 테스트 케이스는 n은 885733, k는 3이다. 3진법으로 바꾸면 1122222222221이 된다. 이때 MAX가 커지면서 noPrime에 들어갈 수 있는 수의 제한이 있어 런타임 에러가 발생했다.

정수 N 이하의 모든 수 중에서 소수를 찾는 문제라면 Math.sqrt 보다는 에라토스테네스의 체가 좀 더 효율적일 수 있지만, 배열 길이가 너무 큰 경우에는 Math.sqrt를 쓰는 것이 낫다는 걸 배울 수 있었다.
</> 끊임없이 성장하기 위해 공부한 내용을 글로 작성하고 있습니다. 틀린 부분이나 추가해야 할 부분이 있다면 언제든 댓글로 남겨주세요❗️
References
'Problem Solving > Programmers' 카테고리의 다른 글
| [프로그래머스] n진수 게임 (0) | 2023.07.12 |
|---|---|
| [프로그래머스] 다트 게임 (0) | 2023.07.06 |
| [프로그래머스] 실패율 (0) | 2023.06.29 |
| [프로그래머스] 뉴스 클러스터링 (0) | 2023.06.29 |
| [프로그래머스] 튜플 (0) | 2023.06.29 |




