| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- JS
- node.js
- 합병 정렬
- state
- 백준
- useState
- 정렬
- 기술면접
- 최소공배수
- 브루트포스
- 코딩테스트
- 코테
- 정규표현식
- 해시
- 자료구조
- 리액트
- sort
- 프로그래머스
- 자바스크립트
- CSS
- BOJ
- 연결리스트
- 딥다이브
- 알고리즘
- 병합 정렬
- Node
- JavaScript
- react
- 완전탐색
- hash
- Today
- Total
가치투자자
[알고리즘] 유클리드 호제법 본문
유클리드 호제법 (유클리드 알고리즘, Euclidean algorithm)
1. 유클리드 호제법이란?
유클리드 호제법 은 두 수 A와 B의 최대공약수를 구하는 알고리즘이다. 여기서 호제법 이란 두 수가 서로 상대방을 나누어 결국 원하는 수를 얻어내는 알고리즘을 말한다.
1-1. 일반적으로 최대공약수 구하기
보통 최대공약수를 구하기 위해 소인수분해 를 사용한다.
22와 8의 경우, 각각 소인수분해하여 최대공약수 2를 구할 수 있다.
22 = 11 x 2
8 = 2 x 2 x 2
그러나 이 방법의 경우, 숫자가 너무 크거나 숫자가 난해한 경우 소인수분해를 하기 어렵다.
1. 수가 너무 큰 경우
: 2304와 1440 => 최대공약수 288
2. 숫자가 난해한 경우
: 403과 155 => 최대공약수 31이런 경우를 해결하고자 유클리드 알고리즘이 탄생했다.
2. 유클리드 호제법의 원리
2-1. 유클리드 호제법 이해하기
유클리드 호제법은 나눈 수를 나머지로 나누는 알고리즘 이다.
두 수가 주어졌을때, 큰 수 A를 작은 수 B로 나누고, 그 다음부터 나눈 수 B를 나머지로 나누고, 나머지가 다시 나눈 수가 된다.
여기서 나머지가 0이 되었을 때, 나눈 수가 A와 B의 최대공약수가 된다.
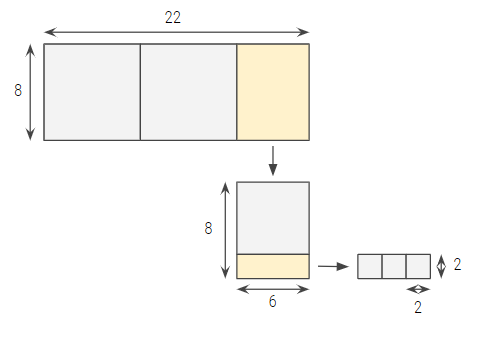
위의 예시를 통해 좀 더 쉽게 설명해보겠다.
22와 8 두 수가 주어졌을 때, 22를 8로 나누면, 몫이 2고 나머지가 6이다.
22 = 8 x 2 + 6그 다음, 나눈 수 8을 6으로 나누면, 몫이 1이고 나머지가 2가 된다.
8 = 6 x 1 + 2또다시 나눈수 6을 2로 나누면, 최종적으로 몫이 3이 되고 나머지가 0이 된다.
그럼 2가 22와 8의 최대공약수가 된다.
6 = 2 x 3 + 0
어떻게 이것이 가능할까? 위 사각형 사진을 함께 참고하면서 이해해보자.
거꾸로 생각한다면, 맨 끝에 나눈수 6은 나머지 2가 3개로 구성되어 있다.
한 단계 올라가서, 나눈수 8은 나머지 6과 2로 구성되어 있고, 그 6은 2개 3개이니 8은 2가 4개로 구성되어 있다.
또 한 단계 올라가서, 22는 8과 6으로 구성되어 있고, 8이 2가 4개, 6이 2가 3개이므로, 22는 2가 11개로 구성되어 있다.
22 = 8 x 2 + 6
6 x 1 + 2
2 x 3 + 0
22 = ((2 x 3) + 2) x 2 + (2 x 3)
한 사각형 안에 정사각형을 잘라내고, 또 남은 사각형에서 또 정사각형을 잘라내다보면 최종적으로 정사각형만 나올때가 온다.
최종적으로 가장 작은 정사각형은 그 위의 모든 사각형 안에 "공통적으로" 들어갈 수 있다.
즉, 맨 마지막에 나머지 2는 그 위의 나머지 사각형인 6의 최대공약수이기도 하고, 또 그 위의 나머지 사각형인 8의 최대공약수이며, 최상위 사각형인 22의 최대공약수이기도 한 것이다.
2-2. 유클리드 호제법 코드
유클리드 호제법을 자바스크립트 코드로 구현하면 다음과 같다.
while (a % b !== 0) {
let rest = a % b // 나머지
if (rest !== 0) { // 나머지가 0일때 그 나머지 출력
a = b; // 나머지를 나눈수에 재할당
b = rest; // 나머지에 새 나머지 할당
}
}
console.log(b); // 최대공약수
3. 관련 문제
- 백준 2609번 - 최대공약수와 최소공배수
https://www.acmicpc.net/problem/2609 - 백준 1934번 - 최소공배수
https://www.acmicpc.net/problem/1934 - 프로그래머스 - N개의 최소공배수
https://school.programmers.co.kr/learn/courses/30/lessons/12953
</> 끊임없이 성장하기 위해 공부한 내용을 글로 작성하고 있습니다. 틀린 부분이나 추가해야 할 부분이 있다면 언제든 댓글로 남겨주세요❗️
References
'Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] LRU 알고리즘 (0) | 2023.06.20 |
|---|---|
| [알고리즘] 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS) (0) | 2023.04.29 |
| [알고리즘] 퀵 정렬 (Quick Sort) (0) | 2023.03.29 |
| [알고리즘] 병합 정렬 (merge sort) (0) | 2023.03.24 |




