Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- JS
- node.js
- 정렬
- 코테
- 브루트포스
- hash
- BOJ
- 합병 정렬
- 자바스크립트
- 병합 정렬
- react
- state
- 기술면접
- 최소공배수
- JavaScript
- 알고리즘
- sort
- 코딩테스트
- Node
- 해시
- 정규표현식
- 리액트
- 딥다이브
- CSS
- 백준
- 완전탐색
- 프로그래머스
- 자료구조
- 연결리스트
- useState
Archives
- Today
- Total
가치투자자
[알고리즘] 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS) 본문
728x90
반응형
DFS와 BFS
그래프는 여러 정점(node)과 그 정점들을 연결하는 간선(edge)으로 이루어진 자료구조다. 그래프나 트리 등 비선형 구조로 데이터가 담긴 자료구조는 순차적으로 나열된 선형 구조(배열, 연결리스트, 스택, 큐)에 비해 데이터 탐색이 훨씬 어렵다. 이러한 그래프의 정점들을 처음부터 끝까지 탐색할 때 대표적인 탐색 방법에는 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)이 있다.
자주 쓰이는 이 두 가지 알고리즘에 대해 쉽게 설명해보고자 한다.
1. 깊이 우선 탐색 (DFS, Depth First Search)
깊이 우선 탐색 (DFS) 은 가장 깊이 있는(끝에 있는)정점까지 다 탐색하고, 다시 갈림길로 돌아와 다른 길로 끝까지 탐색하는 알고리즘이다. 쉽게 설명하자면, 여러 드라마들이 있을때, A라는 드라마를 1편부터 끝까지 다 본 후, B라는 드라마를 1화부터 보는 방식인 것이다.
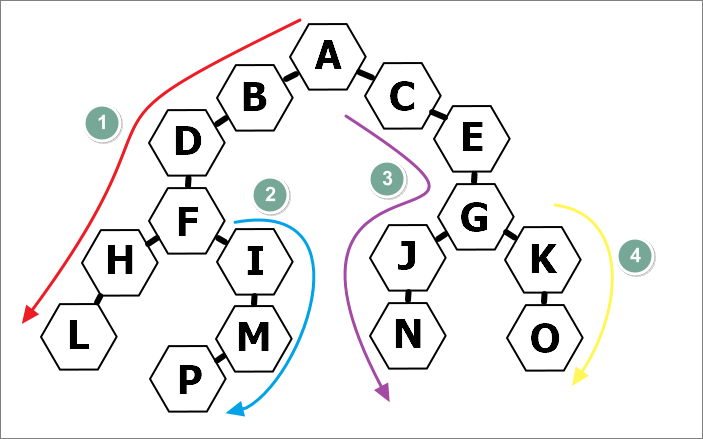
DFS의 특징은 다음과 같다.
- 모든 정점을 탐색하고자 할 때 사용한다.
- BFS에 비해 알고리즘이 더 간단하다.
- 검색 속도는 BFS에 비해 느리다.
- 스택(stack) 또는 재귀함수로 구현
이러한 DFS를 수도 코드로 표현해보면 다음과 같다.
dfs(v: 현재 정점){
if(v를 방문) 리턴;
v 방문한 사실을 저장;
결과 변수 배열 맨 뒤에 v값 삽입;
v와 인접한 정점들의 배열의 첫 번째 정점부터 순서대로
방문하지 않은 정점에 대해 dfs(정점) 호출;
}
반응형
2. 너비 우선 탐색 (BFS, Breadth First Search)
너비 우선 탐색 (BFS) 은 시작점에서 가까운 순으로 모두 탐색한 뒤 다음 데이터를 탐색하는 알고리즘이다. 쉽게 설명하자면, 드라마 A, B, C가 있을 때, 각 드라마의 1화를 하나씩 보고, 그 다음으로 1화 밑에 있는 2화를 다 보는 방식인 것이다.

BFS의 특징은 다음과 같다.
- 주로 두 정점 사이의 최단 경로를 찾을 때 사용한다.
- 큐(queue)로 구현
이러한 BFS를 수도 코드로 표현해보면 다음과 같다.
bfs(vStart: 처음에 방문해야 할 정점){
방문할 정점 배열 = [vStart];
while(방문할 정점 배열의 길이가 0이 될 때까지){
v = 방문할 정점 배열에서 첫 번째 요소를 pop;
if(v 방문){
continue;
}
v 방문 사실 저장;
결과 배열에 v값 push;
v와 인접한 정점 배열의 첫 번째 정점부터
방문하지 않은 정점을 방문할 정점 배열의 끝에 삽입;
}
}
3. 관련 문제
- 백준 1260번 - DFS와 BFS
https://www.acmicpc.net/problem/1260 - 백준 16948번 - 데스 나이트
https://www.acmicpc.net/problem/16948
</> 끊임없이 성장하기 위해 공부한 내용을 글로 작성하고 있습니다. 틀린 부분이나 추가해야 할 부분이 있다면 언제든 댓글로 남겨주세요❗️
References
728x90
반응형
'Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] LRU 알고리즘 (0) | 2023.06.20 |
|---|---|
| [알고리즘] 유클리드 호제법 (1) | 2023.04.13 |
| [알고리즘] 퀵 정렬 (Quick Sort) (0) | 2023.03.29 |
| [알고리즘] 병합 정렬 (merge sort) (0) | 2023.03.24 |




